Kurt Gödel (1906-1978) - Norbert Wiener (1894-1964) -  John Von Neumann (1903-1957) - Alonzo Church (1903-1995) - Alan Turing (1912-1954) - Claude Shannon (1916-2001) - ...

Last update : 11/11/2016

Nous le savons, et pour faire vite, à partir de Galilée et de Descartes, le monde a été conçu selon un modèle qui a permis le développement considérable des sciences et des techniques, en liaison avec l'avènement progressif de la société industrielle. La pensée mécaniste, de Galilée à Newton, définit un Univers caractérisé par sa régularité, son ordre, sa réversibilité, sa prévisibilité. Mais cet espace et ce temps absolu existent sans référence aux choses extérieures, et surtout l'homme est ainsi repoussé hors de la vie et de l'expérience sensible, il devient une sorte de "contemplateur" extérieur au monde.

Par la suite, les XIXe et XXe siècles connaissent des mutations théoriques fondamentales : l'évolutionnisme de Darwin et la thermodynamique de Sadi Carnot portent un premier coup à la science classique, puis la mécanique quantique, la relativité qui bouleverse les concepts traditionnels du temps et de l'espace. La science moderne se caractérise désormais par l'introduction, au sein même de ses objets, de la discontinuité, de la probabilité, du devenir. Ce que Bachelard appellera le "nouvel esprit scientifique", semble reposer la question de la relation de l'homme à son monde, et celui-ci semble plus complexe, tant dans l'infini grand que dans l'infiniment petit. Le ciel qui depuis des millénaires, avait paru échapper au changement, s'inscrit maintenant dans un Univers qui évolue sans cesse. Si l'imagination scientifique ne se prive désormais plus d'enrichir ses hypothèses et ses concepts, de varier les possibilités de questionnement, si la technologie qu'elle génère et qui la sert accroît la maîtrise de l'activité et de la physiologie humaines, assiste-t-on à un renouvellement de nos interrogations fondamentales, l'homme est-il plus ou mieux pensé qu'il ne le fut, un sens de l'existence vient-il à se formaliser aussi nettement que ce qui semble s'opérer dans le domaine des sciences?

 

Bertrand Russell avait déjà formalisé en son temps, au temps de la relativité naissante, une "conception du monde" a minima qui semble ne pas avoir évolué depuis lors : "premièrement, les entités de la physique mathématique n'appartiennent pas à la substance du monde, mais sont des constructions composées d'événements et prises pour unités par le mathématicien pour des raisons de commodité. Deuxièmement, tout ce que nous percevons sans recourir à l'inférence, appartient à notre monde particulier. A cet égard, je suis d'accord avec Berkeley. Le ciel étoilé que nous fait connaître la sensation visuelle est à l'intérieur de nous. Le ciel étoilé extérieur auquel nous croyons est inféré. Troisièmement, les lignes causales qui nous permettent d'avoir conscience de multiples objets, bien que l'on trouve partout de telles lignes, sont susceptibles de disparaître comme des rivières dans le sable. C'est pourquoi nous ne percevons pas tout à tout moment..."

(Works : Osnat Tzadok - The Center of the Universe)

Quand Einstein a énoncé sa célébrissime équation, E=mc2, le monde n'a pas changé, les particules observaient toujours le même comportement et l'homme est resté ce qui'il a toujours été. Ce qui a changé, c'est la vision que l'Humanité se faisait de l'Univers, et dans une moindre mesure l'Homme a posé un autre regard sur lui-même, mais ce regard ne change guère la conception de l'homme sur l'homme et de son existence. Fondamentalement, et pour forcer le trait,  le programmeur informatique préfère communiquer avec des machines plutôt qu'avec ses semblables. Ces quelques centaines d'hommes et de femmes qui jalonnent l'histoire de la science, ont le plus souvent travaillés dans un contexte de conflit et d'instabilité politique, certains ont voulu comprendre les rouages de l'Univers et de la vie, les autres ont exploité les processus fondamentaux pour créer des techniques destinées à améliorer nos conditions d'existence, mais tous ont été d'une manière ou d'une autre rejetés dans l'obscurité ou ignorés au profit d'une énorme et froide récupération politique et sociale.

Pourtant, quelque part, ces avancées scientifiques n'ont pas seulement modifié nos modes de vie, voire nos comportements, mais subtilement envahie nos possibilités de penser notre existence.

Max Weber, Herbert Marcuse, Jürgen Habermas ont successivement mis en évidence le concept de "rationalité" pour décrire cette "institutionnalisation du progrès scientifique et technique" qui pénètre dans tous les domaines de l'existence, urbanise nos modes de vie, technicise nos échanges et nos communications : Marcuse était par exemple convaincu qu'au nom de cette rationalité c'est une "forme déterminée de domination politique inavouée" qui s'impose. Dans les sociétés capitalistes, écrira-t-il, la domination tend à perdre son caractère d'exploitation et de répression pour devenir "rationnelle", et par ce biais s'instaure une "légitimité" de la domination que nous abandonnons "naturellement" pour "des conditions d'existence toujours plus confortables".

L'Univers de la science et de la technique qui se développe et s'accélère considérablement après la Seconde Guerre mondiale et participe à l'effort de reconstruction et de rénovation, quelque part, de nos désirs d'avenir, déplace ainsi subtilement nos interrogations sur le terrain des "conditions de notre existence", et non plus sur "l'existence elle-même".

La technologie informatique, calcul, simulation, communication, combinatoire, créée ainsi une "métapensée", qui n'est pas la pensée, mais un substitut de pensée dont la force est de pouvoir se donner au travers d'un mode de vie immédiat, définir nos relations avec le monde et avec nos semblables, et nous donner un rôle social suffisamment acceptable ..

(Works : Elia Fernández - Universe) 

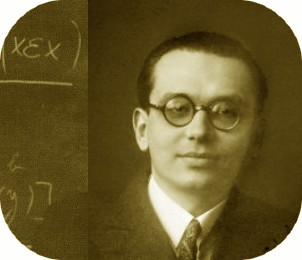
Kurt Gödel (1906-1978)

Toute théorie scientifique se doit d'être présentée en termes mathématiques et l'ordinateur est l'instrument mathématique par excellence. Cette formulation, devenue évidence, s'enracine dans l'approche radicale des mathématiques que sut imposé David Hilbert entre 1888  et 1900 : il va réduire en effet certaines branches des mathématiques à une série d'axiomes se justifiant par eux-mêmes, les mathématiques sont ainsi affranchies de toute relation à une réalité physique, jusqu'à faire reposer sur des bases absolument solides et incontestables l'édifice entier des mathématiques ..

- via la Complétude, toute proposition mathématique vraie doit pouvoir être prouvée à partir d'un ensemble fini d'axiomes et de règles de logique.

- via la Cohérence, le système ne doit jamais permettre de prouver à la fois une proposition et son contraire (ce qui serait une contradiction).

- via la Décidabilité, il doit exister une procédure mécanique (un algorithme) pour déterminer si n'importe quel énoncé est vrai ou faux.

C'était le rêve d'un système mathématique parfait, autosuffisant et infaillible...

 

La notion de "formalisme" traduit le fait que les mathématiques sont une affaire de systèmes symboliques formels dans lequel tous les arguments ont le pouvoir de se justifier par eux-mêmes. Il semble alors d'évidence qu'il ne peut exister de solution à un problème qui ne puisse être résolu par l'intermédiaire de la "pensée pure" : "wir müssen wissen, wir werden wissen"..

 

Existe-t-il des objets non mathématisables?

Notre existence répond à cette question. Mais l'interrogation sur les limites de la formalisation mathématique en tant que processus interne à ces mathématiques a été posée durant tout le début du XXe siècle ... 

 

En 1931, le jeune Kurt Gödel, alors âgé de 25 ans, publie son article qui pulvérise ce rêve. Son génie a été de créer une méthode pour que les mathématiques se parlent d'elles-mêmes. Il a "arithmétisé" le langage mathématique, c'est-à-dire qu'il a codé les énoncés et les preuves avec des nombres. Cela lui a permis de construire un énoncé G qui, une fois décodé, dit essentiellement : "Cet énoncé n'est pas démontrable dans le système."

 

Les Deux Théorèmes d'Incomplétude ...

- Premier théorème : Dans tout système formel suffisamment puissant pour décrire l'arithmétique élémentaire (comme celle qu'on apprend à l'école), il existe des énoncés vrais mais indémontrables à l'intérieur du système. Le système est incomplet.

- Deuxième théorème : Un tel système ne peut pas démontrer sa propre cohérence (le fait qu'il soit sans contradiction).

 

Le théorème de Gödel (1931) met un terme à cet immense optimisme sur la capacité des mathématiques à déboucher sur une théorie du Tout, après, il est vrai, une cinquantaine d'années extraordinairement fécondes: "tout ce autour de quoi nous pouvons dessiner un cercle ne peut s'expliquer sans se référer à quelque chose en dehors du cercle; quelque chose que nous devons supposer, mais que nous ne pouvons pas prouver." 

 

Une théorie suffisamment cohérente doit obligatoirement contenir des propositions qui ne sont pas décidables ...

Gödel reprend le paradoxe du menteur (si vous êtes menteur, alors le fait de dire que vous mentez est en soi un mensonge) pour le transformer une une théorie prouvant qu'il existe des limites à ce qui peut être affirmé par les mathématiques. Et Gödel montre qu'il peut exister des axiomes vrais sur les nombres sans que l'on puisse les prouver en appliquant des séries de règles. 

 

Pour étendre ces fameux théorèmes de l'incomplétude, on ne peut donner un sens à l'univers sans donner de l'existence à quelque chose en dehors de lui. Autrement dit,  la vérité est plus importante que la démonstration...

Ces théorèmes sont publiés dans ses deux ouvrages, la "Complétude des axiomes du calcul fonctionnel" (1930) et  "Sur les énoncés formellement indécidables des « Principa Mathematica » et des systèmes connexes" (1931). 

 

Kurt Gödel naquit à Brno, l'ancienne capitale de la Moravie, et immigra aux Etats-Unis en 1940 : il ne put jamais parvenir à construire le système philosophique qu'il espérait tant et, hypocondriaque, mourut à 73 ans de sous-alimentation. "La vie telle que nous la connaissons pourrait ne pas être l'existence totale de l'individu. Peut-être se poursuit-elle dans un autre monde...."  Pour le commun des mortels, la révélation de contradictions au sein des mathématiques n'aura aucune conséquence. . .visible.

 

 "Incompleteness: The Proof and Paradox of Kurt Gödel", Rebecca Goldstein (2005)

Goldstein, elle-même philosophe et romancière, ne se contente pas de raconter les événements de la vie de Gödel (son enfance à Vienne, son amitié avec Einstein à Princeton, sa paranoïa, sa mort tragique). Elle réussit l'exploit de rendre accessibles ses idées révolutionnaires et de montrer comment elles sont inextricablement liées à sa personnalité et sa vision du monde. Elle explique les théorèmes d'incomplétude avec une clarté remarquable, sans formules mathématiques complexes, en se concentrant sur leur signification profonde.

Ce n'est pas non plus une simple chronique. Goldstein plonge dans la psychologie de Gödel – son platonisme mathématique (sa conviction que les objets mathématiques existent dans un monde idéal), son rationalisme extrême, ses angoisses et son obsession pour la précision et la propreté. Elle montre comment ce même esprit, capable d'une abstraction et d'une rigueur extraordinaires, était aussi vulnérable à des peurs irrationnelles.

Elle parvient à situer Gödel dans son époque, au cœur des bouleversements intellectuels du XXe siècle. Le livre explore ses relations avec les autres géants de son temps, notamment son amitié profonde et touchante avec Albert Einstein à l'Institute for Advanced Study de Princeton. Le portrait de ces deux esprits géniaux, si différents (l'un tourné vers le cosmos, l'autre vers l'univers des mathématiques pures), est fascinant.

L'ouvrage a été traduit et publié en français sous le titre "Kurt Gödel : Une vie de la raison", aux Éditions Philippe Rey .

Si le livre de Goldstein s'impose comme le plus accessible et le plus complet pour un public général, il existe d'autres ouvrages de référence ...

- "Kurt Gödel: The Genius of Incompleteness" de John W. Dawson Jr. (1997) : Dawson est l'éditeur des œuvres complètes de Gödel et l'un de ses biographes académiques les plus respectés. Son travail est plus technique et détaillé, s'appuyant sur une étude exhaustive des archives. C'est la biographie "savante" de référence, mais elle est moins narrative et peut-être moins engageante pour un premier contact.

- "A Logical Journey: From Gödel to Philosophy" de Hao Wang (1996): Wang était un logicien et un collègue de Gödel à Princeton qui a eu de longues conversations avec lui. Ce livre est une source primaire précieuse, transcrivant les opinions philosophiques souvent surprenantes de Gödel sur tous les sujets. C'est un complément fascinant, mais il vaut mieux le lire après une biographie générale comme celle de Goldstein.

Deux ouvrages non traduits en français.

Le Séisme de l'Incomplétude ...

Le théorème de Gödel est l'aboutissement d'une quête millénaire de certitude et de rigueur.

Ce n'est pas une faille dans la raison, mais une découverte sur la structure même de la rationalité ...

Il nous dit que l'univers de la connaissance est ouvert, infini et qu'il contient toujours une part de mystère. Il nous libère de l'illusion d'un système parfait et clos, et nous invite à une quête de connaissance toujours renouvelée, consciente de ses propres limites mais non diminuée par elles. C'est pour cette raison profonde qu'il reste un sommet inégalé de la pensée humaine.

 

L'impact de cette mis en évidence fut comparable à un tremblement de terre intellectuel pour plusieurs raisons ...

- La Fin de la Certitude Absolue : Gödel a montré qu'aucun système logique un peu complexe ne pouvait à la fois être complet (tout prouver) et cohérent (ne pas se contredire). Il faut choisir. Les mathématiques, considérées comme le langage de la certitude par excellence, contenaient en leur cœur des vérités inaccessibles par la démonstration.

- Les Limites Intrinsèques de la Raison Formelle : Il a établi une limite fondamentale à ce que la logique et le calcul formel peuvent accomplir. Il y a des questions qui, par nature, échappent à la démonstration à l'intérieur d'un système donné. La vérité dépasse la démonstrabilité.

- L'Effondrement du rêve hilbertien : Le programme de Hilbert, qui visait à sécuriser tout l'édifice mathématique, était tout simplement impossible. L'idée de pouvoir un jour "terminer" les mathématiques en résolvant tous les problèmes s'est évaporée.

- Un Changement de Paradigme : On est passé d'une vision où les mathématiques étaient une forêt qu'on pouvait défricher entièrement, à une vision où c'est un univers infini et insondable, avec des "trous" de vérité que nous ne pourrons jamais combler de l'intérieur.

 

Les implications du théorème de Gödel vont bien au-delà des mathématiques pures et touchent à la philosophie, à l'informatique et à notre vision du monde...

 

1.- En Mathématiques et Logique ...

Les mathématiciens ont accepté l'incomplétude. Ils travaillent avec des systèmes qu'ils savent incomplets, en essayant de les renforcer si nécessaire (en ajoutant de nouveaux axiomes), mais sachant que le problème se posera à nouveau. Cela a ouvert tout un champ de recherche sur la force relative des systèmes formels et la nature de la démonstration.

 

2. - En Informatique et Intelligence Artificielle ...

Le théorème est directement lié au problème de l'arrêt d'Alan Turing (est-ce qu'un programme va s'arrêter ou tourner à l'infini ?). Turing a montré qu'il n'existe pas d'algorithme capable de résoudre ce problème pour tous les programmes. C'est une forme d'incomplétude algorithmique. Cela emporte tout autant des limites fondamentales à l'informatique même : certains problèmes sont indécidables, c'est-à-dire qu'aucun ordinateur, aussi puissant soit-il, ne peut les résoudre. 

Et en IA, cela a alimenté le débat : un système formel (comme un programme d'IA) peut-il comprendre ou reproduire l'intelligence humaine dans son intégralité ? Gödel suggère que la pensée humaine, capable de percevoir la vérité d'un énoncé indémontrable, possède une qualité qui échappe aux systèmes formels fermés.

Des travaux qui ont alimenté le débat sur la possibilité d'une intelligence artificielle forte. Si l'esprit humain peut percevoir des vérités qu'une machine formelle (suivant un système axiomatique) ne peut démontrer, cela suggère une différence fondamentale entre cognition humaine et computation (argument développé par des philosophes comme Roger Penrose).

 

3.- En Philosophie et Epistémologie (Théorie de la Connaissance) ...

- Contre le Réductionnisme : C'est un argument puissant contre les visions purement mécanistes ou computationnelles de l'esprit et de l'univers. Le tout est plus que la somme des parties, et certains systèmes ne peuvent pas se comprendre entièrement eux-mêmes.

- Humilité Intellectuelle : Le théorème nous enseigne l'humilité. Aucun système de pensée, aussi élaboré soit-il, ne peut prétendre à l'exhaustivité et à l'autosuffisance totale. Il y aura toujours des vérités qui lui échappent.

- La Nature de la Vérité : Il établit une distinction cruciale entre la vérité et la démontrabilité. La vérité existe objectivement, mais notre accès à elle, par la démonstration formelle, est limité. Cela réhabilite en un sens l'intuition et la conscience comme moyens d'accéder à la connaissance.

- Un renforcement du "platonisme" : Gödel interprétait ses résultats comme une preuve de l'existence d'une réalité mathématique objective indépendante de l'esprit humain (platonisme), car des vérités existent même si elles sont inaccessibles par nos systèmes formels.

- Postmodernisme : L'idée qu'aucun système (linguistique, social, idéologique) ne peut être complet ou totalement cohérent résonne avec la pensée postmoderne qui déconstruit les grands récits et les certitudes absolues.

- Science-Fiction et Fiction Conceptuelle : Des auteurs comme Stanisław Lem ou Jorge Luis Borges (dans un sens plus large) explorent les paradoxes, les réalités incomplètes ou les systèmes qui s'autodétruisent par leur logique même, échos des idées gödéliennes.

Alan Turing (1912-1954)

En 1935, Turing entend parler du problème de la décidabilité (Entscheidungsproblem) posé par le mathématicien allemand David Hilbert, l'initiateur d'une approche radicale des mathématiques, le formalisme, et l'homme qui stupéfia Paris en 1900 en présentant ses vingt-trois problèmes mathématiques, dont certains n'ont pas encore été résolus.

Peut-on trouver une méthode formelle permettant de déterminer si une affirmation mathématique est prouvable, quelle qu'elle soit? Pour répondre à cette interrogation, Turing se porte sur les mécanismes intellectuelles que ses contemporains mettent en oeuvre, exprime cette approche sous l'angle d'une machine théorique, susceptible d'effectuer des opérations élémentaires précisément définies, en déchiffrant et en écrivant des symboles sur un ruban perforé. C'est au fond la naissance de l'algorithme.

Pour Turing, la réponse à la question de Hilbert est négative, mais il a ainsi montré qu'un algorithme peut servir à résoudre un problème, et qu'il est possible de construire une machine obéissant à un algorithme spécifique.  Turing, pour faire bref, vient de créer la structure intellectuelle permettant d'écrire un programme informatique (On Computable Numbers, with an application to the Entscheidungs Problem, 1936). 

Alan Turing, "père de la science informatique moderne", inventeur du test dit de Turing permettant de définir les critères d'une "machine intelligente", concepteur de la machine électromécanique qui contribua à déchiffrer les codes secrets de la machine nazie Enigma (1939), meurt à 42 ans après avoir été incarcéré pour son homosexualité et obligé à recevoir des injections d'hormone d'oestrogène.

Andrew Hodges a publié en 1983 "Alan Turing: the enigma of intelligence" : en Turing cohabitent une sensibilité douloureuse, une curiosité sans nom pour la perception extrasensorielle, et une intelligence hors du commun.

 

Fasciné par l'embryogenèse et la morphogénèse, - comment chaque cellule sait-elle ce qu'elle doit faire pour donner à l'organisme la symétrie attendue -, hanté par le problème de la relation corps-esprit, il n'aura pourtant pas la possibilité, ou les ressources nécessaires, de "penser la pensée", et se focalisera uniquement sur la définition opérationnelle de celle-ci....

"Alan Turing: The Enigma", Andrew Hodges (1983)

Biographie Incontournable sur Alan Turing, ouvrage de référence, c'est une œuvre monumentale et définitive. Hodges, un mathématicien lui-même, a mené un travail de recherche colossal, s'appuyant sur des archives et des témoignages directs. Il couvre toute la vie de Turing, de son enfance à sa mort tragique.

La grande force de ce livre : Hodges explique avec clarté les concepts fondamentaux de l'informatique, de la cryptanalyse et de l'intelligence artificielle, tout en tissant un récit profondément humain et poignant de la vie personnelle de Turing, de son homosexualité, de sa personnalité singulière et de la persécution qu'il a subie.

Le titre, "The Enigma", fonctionne sur plusieurs niveaux : c'est la machine que Turing a contribué à cracker, mais c'est aussi l'énigme que cet homme complexe a représenté pour ses contemporains, et le mystère entourant sa mort. Ce livre sera la source principale qui inspirera de nombreuses œuvres ultérieures, dont le film à succès "The Imitation Game" (2014). Bien que le film prenne des libertés avec la réalité, le livre de Hodges reste la pierre de touche de la vérité historique.

Sa traduction en français, "Alan Turing : Le Génie qui a inventé l'ordinateur et déjoué les codes secrets nazis" (Éditeur Payot). 

Parmi d'autres ouvrages notables sur Turing ...

- "Alan Turing: His Work and Impact" (sous la direction de S. Barry Cooper et Jan van Leeuwen) : C'est un ouvrage plus technique et académique, rassemblant des articles de Turing et des commentaires sur son impact dans tous les domaines (informatique, intelligence artificielle, biologie mathématique, etc.). C'est un complément idéal pour qui veut approfondir son œuvre scientifique.

- "The Annotated Turing: A Guided Tour Through Alan Turing's Historic Paper on Computability and the Turing Machine" par Charles Petzold : Un livre génial qui décortique et explique pas à pas l'article historique de 1936 de Turing, ce qui le rend accessible à un public non spécialiste.

- "Alan M. Turing" par Sara Turing : La biographie écrite par la mère de Turing. C'est un témoignage touchant et personnel, mais bien sûr, elle occulte complètement son homosexualité et est bien moins critique que le travail d'historien d'Hodges.

Norbert Wiener (1894-1964)

Norber Wiener, intelligence précoce, né à Columbia, part étudier la logique à l'université de Cambridge avec Bertrand Russell, puis David Hilbert qu'il rejoint en Allemagne. C'est à partir de 1919, au Massachusetts Institute of Technology, qu'il trouve sa voie. Pour lui, biologie et mathématiques, qui semblent poursuivre des objectifs différents, peuvent être associées dans une nouvelle approche.

Etudiant les systèmes de contrôle et de communication opérant dans l'animal et dans la machine, Wiener introduit le concept selon lequel les systèmes ont des inputs et des outputs qui sont influencés par des mécanismes de feed-back ou rétroaction.

Lors de la Seconde Guerre mondiale, mettant au point de nouveaux systèmes de défense aérienne, il étudie le couple homme-machine, les mécanismes de réception et de remontée de l'information et en vient à définir avec précision les éléments d'un autocontrôle précis. Il conforte ainsi l'importance de la notion de feed-back et positionne la "communication" comme le ciment de toute structure à organisation complexe.

En 1948, Wiener publie "Cybernetics, or Control and Communication in the Animal and the Machine" qui marque la naissance de la "Cybernétique". Le monde est centré sur l'information, plus que sur l'énergie, sur les processus digitaux plus que sur les processus analogiques. 

Sous le maccarthysme (1950-1954), Norbert Wiener fut l'objet d'une surveillance constante, abandonna toute recherche et s'enferma dans une réflexion utopique sans lendemain, traumatisé par les effets de la guerre et l'impossibilité de contrôler l'usage qui était fait de la recherche scientifique. Il s'était toujours élevé contre les déclarations excessives de certains inconditionnels de la cybernétique, dont le succès fut alors phénoménal  : " ... en sorcellerie, on doit toujours demander ce qu'on veut vraiment et non quelque chose qu'on semble vouloir. C'est la même chose avec l'automatisme moderne ; il est très facile de demander ce qu'on pense vouloir et qu'on ne veut pas. C'est un danger réel, spécialement de nos jours, quand il y a la possibilité d'employer les machines qui apprennent, qui jouent le jeu de la guerre, pour contrôler quand on doit pousser le bouton déclenchant une guerre mondiale. Le seul moyen de l'éviter est de considérer la machine non comme but en soi-même mais comme un moyen de satisfaire les demandes de l'homme, comme une partie d'un système humano-mécanique."

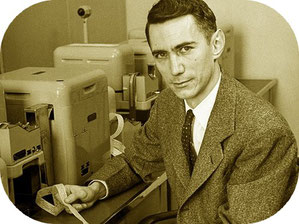
Claude Shannon (1916-2001)

L'ordinateur est un outil de traitement de l'information, pour cela il a fallu se pencher sur la nature même de cette information. La théorie établie par Claude Shannon repose sur la distinction entre ce qui susceptible d'être prédit, et ce qui ne peut pas l'être et qui ainsi constitue la véritable information.  

Né à Gaylord (Michigan), Claude Elwood Shannon obtient en 1940 un master en ingénierie électrique et un doctorat en mathématique du Massachusetts Institute of Technology, et  c'est en 1941 qu'il rejoint les Bell Telephone Laboratories pour développer des méthodes de transmission de l'information et améliorer la disponibilité du téléphone à longue distance. Et la communication commence par l'information. "Le problème fondamental de la communication est la reproduction en un point, de façon fidèle ou approximative, d'un message sélectionné en un autre point."

En 1948, alors que tout le monde pense qu'une transmission sur un câble doit nécessairement utiliser une onde électromagnétique, Shannon propose d'utiliser un système de codage entre la source et le canal de transmission ainsi qu'un décodeur entre le canal et le récepteur, et ceci à l'aide d'un commutateur générant un flux de 0 et de 1.  En associant cette notion de commutateur à l'algèbre de Boole, Shannon montre que l'information peut être traitée automatiquement par les circuits électriques.

Shannon tentera d'étendre cette découverte aux systèmes biologiques (Algèbre pour la génétique théorique, 1939). Puis,  il n'aura de cesse d'appliquer son esprit scientifique à la réalisation de multiples machines en tout genre (Theseus, la souris magnétique capable de se diriger dans un labyrinthe, 1950; des machines à jongler, des programmes d'échecs...), jusqu'à inventer une machine "sans finalité", dont la mise en route provoque son arrêt.  La maladie d’Alzheimer le conduisit au Courtyard Nursing Care Center de Medford, Mass. où il mourra le 24 février 2001.